Toda la información de este capítulo ha sido extraída de: http://www.diac.upm.es/asignaturas/sistaudio/TFC Ignacio/index.html Página no disponible actualmente.
2.1-Frecuencia, módulo y fase.
2.2-Espectro.
2.1 FRECUENCIA, MODULO Y FASE
La frecuencia de oscilación de una partícula (o de cualquier magnitud, como por ejemplo el voltaje de una señal eléctrica) es la cantidad de ciclos completos en un tiempo dado. La frecuencia se mide en hertzios (Hz.), e indica el número de ciclos completos en un segundo. Un ciclo es el recorrido completo que efectúa una partícula desde su posición central, hasta otra vez esa misma posición, habiendo pasado por su posición de desplazamiento máximo y mínimo.

Los sonidos de una única frecuencia, se llaman tonos puros. Un tono puro se escucha como un «pitido», el timbre dependerá de la frecuencia que lo genere. El sonido que se escucha en el teléfono antes de marcar, por ejemplo, corresponde a un tono puro de frecuencia cercana a 400 Hz. El tono de la «carta de ajuste» de la televisión, corresponde a una frecuencia de 1000 Hz.
La posición de una partícula en un instante de tiempo concreto, dependerá de tres factores: frecuencia, módulo y fase. La frecuencia ya se ha definido. El módulo indica la amplitud de la oscilación, si se trata de partículas que se mueven, el módulo estará definido en metros (m), si se trata de una señal eléctrica, el módulo estará definido en voltios (V). En el siguiente ejemplo se tienen dos partículas que realizan ciclos completos (hacen un ciclo y paran). Las dos oscilan con igual frecuencia, pero varía la amplitud, ya que el módulo de la partícula II es mayor que el módulo de la partícula I.
 |
|
La fase indica la posición de la partícula que oscila en el momento de empezar a contar el tiempo, es decir en T = 0 s. La fase se mide en radianes (rad) o en grados (º). 360º = 2π rad. Si calculamos el coseno de la fase, nos da un valor entre 1 y -1. Viendo las partículas I y II, «1» significaría que la partícula estaba a la derecha del todo, «-1« a la izquierda del todo.
Se habla de fase relativa cuando lo que interesa es la diferencia que existe entre dos movimientos de la misma frecuencia. Si dos partículas u ondas se mueven con igual frecuencia, pero cuando una pasa por cero, la otra no lo hace o lo hace en dirección contraria, tendrán una fase relativa distinta de cero. Exactamente si cuando una pasa por cero, la otra lo hace en dirección contraria, tendrán una fase relativa de 180º (grados) o de π radianes. En este caso, si las dos ondas tienen igual módulo, se cancelarán una a la otra, siendo el resultado total cero. Si dos manos tratan de mover con igual fuerza una hoja de papel, cada una desde un lado, con fase relativa cero, el desplazamiento de la hoja será máximo. Es decir, cuando una empuja la otra recoge (las dos pasan por cero en el mismo momento y misma dirección). Si lo hacen con fase relativa 180º, el desplazamiento será nulo.
El «periodo» (T) es el inverso de la frecuencia (T=1/f). El periodo se mide en segundos (s). Según esta definición, en el ejemplo de las tres partículas en movimiento. la primera tiene un periodo de 4 segundos, en la segunda T=2 s. y en la tercera T=1 s.
Cualquier sonido (voz, música, ruido…) está compuesto por múltiples frecuencias. Se puede descomponer el sonido en múltiples tonos puros. Si un sonido cambia con el tiempo, la amplitud y fase de cada tono puro o frecuencia en que se descompone ese sonido, también variará con el tiempo.
2.2- ESPECTRO.
El espectro es la representación de las frecuencias que componen una señal de audio y se obtiene calculando la energía que aporta cada frecuencia al sonido total. Normalmente la representación no se hace en términos de energía directamente, sino que se calcula el nivel (10Log) respecto a la energía de referencia. Con esto se obtiene el «Nivel espectral» expresado en dB. Aunque el proceso de cálculo es bastante tedioso, la electrónica e informática actuales, con hardware o software que trabajan con procesos TFT y FFT, simplifica enormemente el trámite, por lo que no se dará más información en este sentido.
Como curiosidad, comentar que en la década de los 80’s, para calcular el nivel espectral de una señal de audio de escasa duración se requerían varios minutos o incluso horas y potentes ordenadores. Actualmente todos estos cálculos se implementan en procesadores y plugins capaces de mostrar los resultados en tiempo real.
De cara a emplear menos recursos y menos tiempo de cálculo, no se calcula en nivel espectral para cada frecuencia (cerca de 20.000) sino que éstas se agrupan en bandas, dando lugar a la representación en «bandas de frecuencia».
Las siguientes figuras muestran representaciones espectrales de un sonido indeterminado (en un instante concreto) cuyo espectro completo está representado en la figura de abajo. La figura central muestra el espectro representado en bandas de media octava y la figura de arriba en bandas de una octava. Las representaciones en octavas suelen contar con 10 bandas y las de media octava con 20. También se utilizan las de tercio de octava (30 o 31 bandas). Las representaciones se hacen sobre ejes de frecuencia logarítmicos, esto hace que en la representación se vea la misma distancia entre las frecuencias 100 Hz y 200 Hz que entre 1 KHz y 2 Khz.

32 63 125 250 500 1K 2K 4K 8K 16K

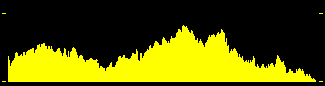
Los números representan las frecuencias centrales expresadas en Hz.
Para los tres casos el espectro está representado de 20 a 20.000 Hz.
La relación que existe entre frecuencias centrales es la siguiente: en bandas de octava: f2 = 2 · f1. En bandas de media octava: f2 = 21/2 · f1. En bandas de tercio de octava: f2 = 21/3 · f1. Siendo f1 la frecuencia central de una banda y f2 la frecuencia central de la banda superior contigua.
La representación espectral (o el espectro) puede resultar muy útil si se sabe interpretar. Básicamente aporta información sobre cuanto contribuye cada frecuencia o cada banda de frecuencia al sonido total. Dicho de otra forma, el espectro permite «ver» el sonido que le llega al oído. Otra cosa diferente será lo que el oído escucha (interpreta).

muy bueno es de mucha ayuda para quienes estamos en los primeros pasos del conocimiento, me encantarìa saber si hay alguna forma de descargar este material para estudiarlo sin necesidad de estar todo el tiempo conectado a la web. desde ya muchas gracias por tan buena informacion un abrazo desde uruguay
Hola Adolfo. Gracias por sus comentarios.
Le informo de los enlaces para la compra y descarga de los manuales:
La edición técnica (los 10 primeros capítulos):
https://www.estudiomarhea.net/manuales-de-sonido-edicion-tecnica-en-pdf-ya-disponible/La edición aula (ecualización, reverb, dinámica y panorámica):
https://www.estudiomarhea.net/manuales-de-sonido-edicion-aula-en-pdf-ya-disponible/Estas ediciones están ampliadas con respecto a la edición online. También desde esos enlaces tiene la posibilidad de descargar versiones promocionales de los manuales, para que pueda ver algunas de sus páginas.
Un cordial saludo.
Hola Adolfo.
Hemos revisado algunas cosas y te muestro los enlaces nuevos:
Edición Técnica Completa. https://www.estudiomarhea.net/manuales-de-sonido-edicion-tecnica-completa-2015/
Edición Aula Completa. https://www.estudiomarhea.net/manuales-de-sonido-edicion-aula-2015/
Y una interesante novedad: Edición Técnica Free. https://www.estudiomarhea.net/manuales-de-sonido-edicion-tecnica-free-online-2015/
Un cordial saludo.
que bárbaros hay muchas cosas enriquecedoras en este manual ojala pudieran hacer una versión a la venta de toda esta información
Hola Samuel. Si te fijas en las cabeceras de cada tema, tienes la opción de compra. Tienes opción de compra individual y la de un pack de 10 temas.
Te dejo la entrada del blog correspondiente a la edición técnica:
https://www.estudiomarhea.net/manuales-de-sonido-edicion-tecnica-en-pdf-ya-disponible/
Y esta es la entrada que anuncia una nueva edición:
https://www.estudiomarhea.net/proximamente-nuevos-pdf/
Un cordial saludo.
es lo que ase mucho tiempo buscaba y mis felicitaciones quisiera que me manden a mi correo el manual gracias
Al menos de momento no contemplamos crear una versión “pdf”. Hay muchos motivos para ello. De momento estamos integrando las páginas del manual en el nuevo formato de nuestro Sitio Web y al mismo tiempo vamos revisando su contenido (gracias a algunos usuarios hemos descubierto algunos errores de contenido ).De momento seguirá estando el manual disponible de forma gratuita en nuestro Sitio Web. Muchas gracias por los comentarios.
https://www.estudiomarhea.net/manuales-de-sonido-edicion-tecnica-en-pdf-ya-disponible/
https://www.estudiomarhea.net/proximamente-nuevos-pdf/
No saben lo que significa para mi esta página con todo lo que tiene, no dejen de hacerla, por favor, gracias por este espléndido trabajo!!